In this blog I explain the algorithm at the core of Cycles, Multilateral Trade Credit Set-off or MTCS [1], in intuitive terms. MTCS is about multilateral clearing in B2B obligation networks, i.e. networks of invoices or debts. It turns out that a significant portion of the total debt (the sum of all the invoice amounts in the network) can be cleared without any money.
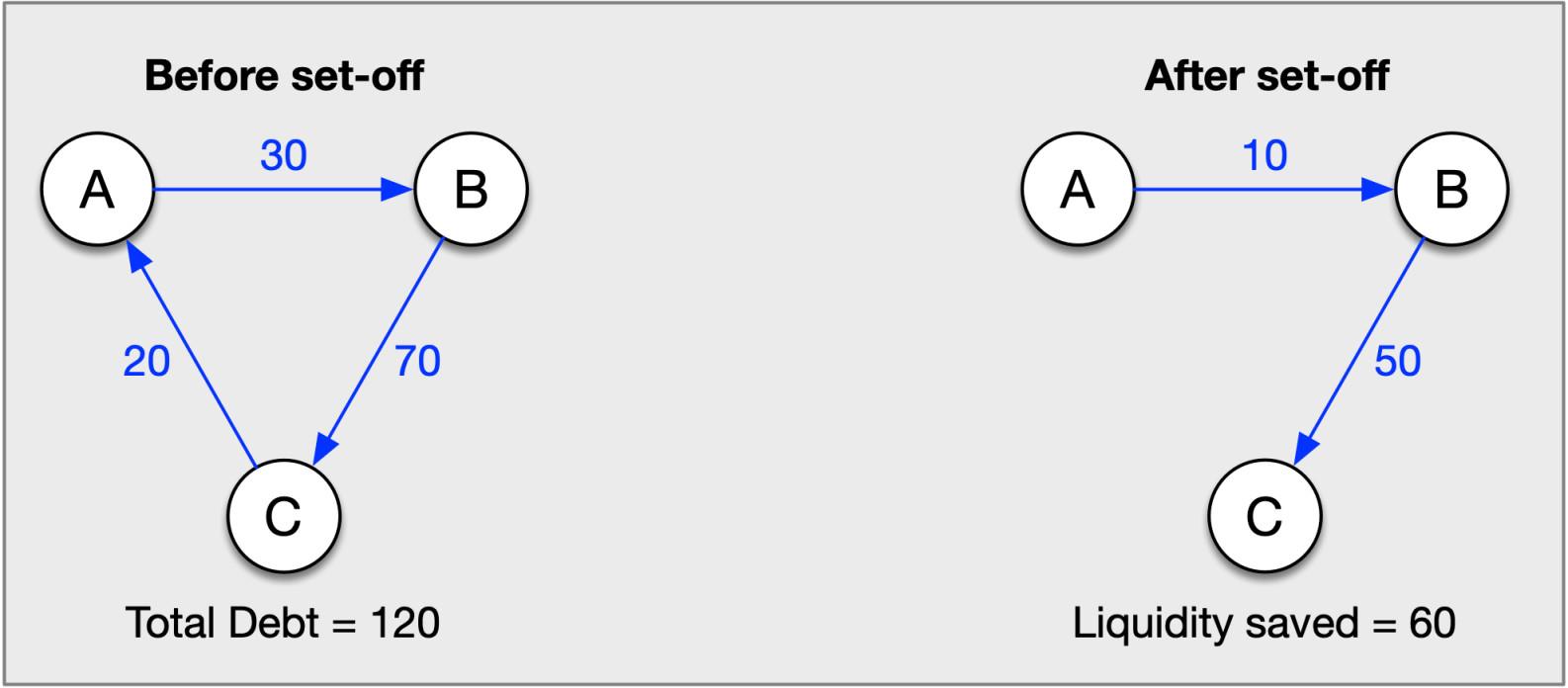
Fig. 1 shows a simple example of three firms, whose mutual obligations form a closed cycle. It turns out that these debts can be cleared using a liquidity amount equal to only 1/2 of the total debt. As shown on the right of the figure, in fact, by subtracting the smallest amount from all three obligations the net position of each company does not change. In other words, the amount that each company has to pay out or that it is receiving is the same before and after the clearing step.
Figure 1: Example obligation network composed of three firms, showing the partial discharge of the obligations by set-off.
The MTCS algorithm was originally executed by merchant bankers manually at the payment fairs in the Renaissance and late Middle Ages [2][3][4][5]. As the merchant bankers became proper banks, they continued the practice among themselves, to this day, but stopped supporting external networks of companies. With the rise of computing, MTCS algorithms began to emerge in the payment system of Yugoslavia. An early reference to this system is [6], which set the basic approach. Slovenia, roughly since its independence, operated an MTCS system at the national scale [1]. Some version of obligation-clearing is being used also in Romania [7] and Bosnia-Herzegovina [8]. Other work on an MTCS-like algorithm is discussed in [9]. The mathematics of our approach is described in [10]. Here we provide a short intuitive summary.
Given a set of \(n\) firms, any obligations existing between them will form an obligation network such that one subset of the firms will necessarily be composed of debtor firms and its complement will necessarily be composed of creditor firms. For each debtor firm, the difference between the incoming obligations (credits) and outgoing obligations (debts) equals a negative net position (\(total\ credits - total\ debts < 0\)) [11]. Creditor firms likewise have positive net positions [12]. The imbalance implied by the different signs of the net positions in these two subsets disappears when all debts are settled. MTCS is based on the observation that, in most cases, the amount of liquidity needed to balance the graph, called 'net internal debt' (NID), is less than the total debt. The difference is composed of closed cycles of obligations that necessarily do not affect the net positions of the firms because for each cycle the weights of its edges are all equal. The set of all such closed cycles is called a 'cyclic structure', and its weight is the amount of liquidity that can be saved.
The minimum-cost, maximum-flow algorithm from graph theory [13] that MTCS uses decomposes a given obligation network into two sub-networks: an acyclic component and the cyclic structure. To ensure that the cyclic structure is the largest possible, the acyclic component is defined as the shortest-path acyclic flow that carries the least amount of liquidity needed to settle all the debts from the debtor firms to the creditor firms, i.e. the NID. Since by construction such a flow settles all the debts, the remaining component has no effect on the net positions. Therefore, it must be purely cyclic: it is the cyclic structure and represents the largest possible liquidity savings. 'Maximum flow' in the algorithm’s name refers to the requirement of the acyclic flow to clear all the debts, i.e. it must equal at least the NID; but it can't be greater because we want to use as little liquidity as possible.
As shown in Fig. 2, such a flow can be imagined to be issuing from a fictitious liquidity source \(v_0\) as a node external to the obligation network and connected to each node \(v_i\), where \(i\) spans from 1 to \(n\), with a new set of directed edges. For each firm, the weight of the new edge corresponds to the firm's net position. The direction is from \(v_0\) to the node if its net position is negative (it needs to draw on the liquidity source) and vice versa if it is positive (it expects excess liquidity to deposit back to the source). The figure shows how the fictitious liquidity source can be split for greater clarity into two auxiliary nodes, one that acts as a source and the other as a sink. 'Minimum cost' is a graph theory term rather than an economic term and it refers to the shortest path of such a maximum flow through the network. The shortest path necessarily rules out all the loops since they imply redundant detours. Subtracting this optimized, acyclic, minimum-cost maximum flow (without the links to and from the fictitious source) from the original obligation network yields the cyclic structure, from which the set-offs to be sent to all the firms are obtained.
Figure 2: The red nodes (net debtors) draw from the fictitious source, and the blue nodes (net creditors) deposit to the fictitious source
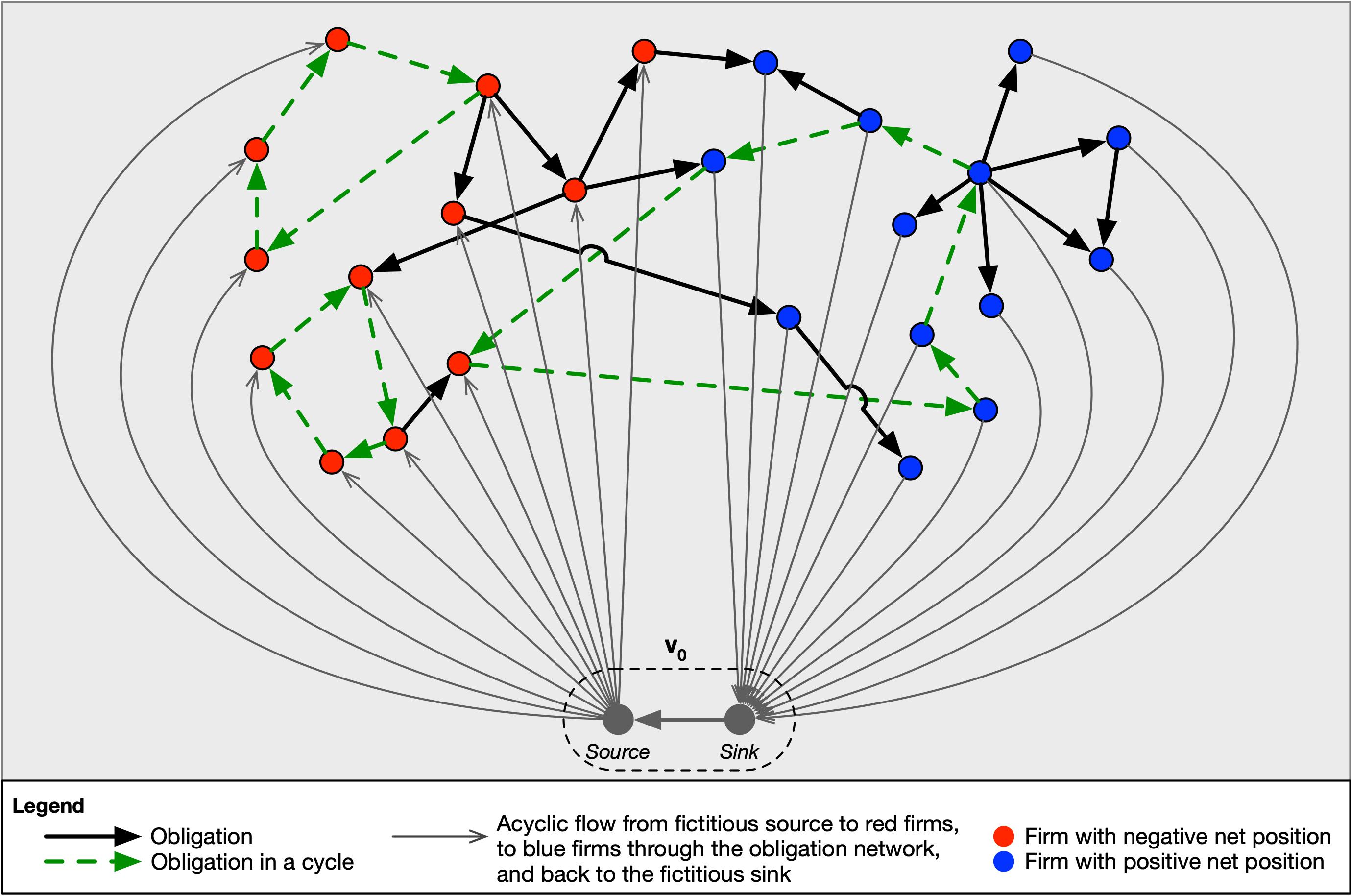
In the very simplified example shown in Fig. 2, the debt that can be cleared without liquidity corresponds topologically to the three cycles shown with dashed green arrows. The weight of each edge belonging to the cyclic structure constitutes the set-off notice, or decrease in obligation amount, that needs to be sent to the two companies defining that edge. This is the amount of liquidity saved or cleared, i.e. which does not have to be paid by the debtor.
Notably, the optimal solution to this minimum-cost maximum-flow problem is not unique. There are in general many optimal paths satisfying the min-cost max-flow problem, thus requiring some means of discerning between them. There are also distinct ways of defining the optimization problem itself (total amount of debt, total number of participants that benefit, etc.). Since we are talking about discharging debts, the solution has real economic consequences, and must thus be treated appropriately. While randomness could be used to pick between solutions, it would be better to enable other solutions to be expressed, for instance through direct governance, or some kind of preference system (e.g. a community could bias the algorithm towards non-profits to benefit from more set-off).
[1] Fleischman, Tomasz and Dini, Paolo and Littera, Giuseppe (2020). Liquidity-Saving through Obligation-Clearing and Mutual Credit: An Effective Monetary Innovation for SMEs in Times of Crisis. Journal of Risk and Financial Management, 13(12), 295.
[2] Amato, Massimo and Fantacci, Luca (2012). The End of Finance. Cambridge: Polity.
[3] Boerner, Lars and Hatfield, John William (2017). The Design of Debt-Clearing Markets: Clearinghouse Mechanisms in Preindustrial Europe. Journal of Political Economy, 125(6): 1991-2037.
[4] Boyer-Xambeu, Marie-Therese and Deleplace, Ghislain and Gillard, Lucien (1994). Private Money & Public Currencies: The 16th Century Challenge. London: Routledge.
[5] Poitras, Geoffrey (2009). From Antwerp to Chicago: the History of Exchange Traded Derivative Security Contracts. Revue d'Histoire des Sciences Humaines, 20(1): 11-50.
[6] Simic, Slobodan and Milanovic, Vladan (1992). Some Remarks on the Problem of Multilateral Compensation. Publikacije Elektrotehnickog fakulteta. Serija Matematika, 22-33.
[7] Gavrila, Lucian-Ionut and Popa, Alexandru (2021). A novel algorithm for clearing financial obligations between companies: An application within the Romanian Ministry of economy. Algorithmic Finance, 9(1-2): 49-60.
[8] Bozic, Milan and Zrnc, Jurica (2022). The Trade Credit Clearinghouse: Liquidity and Coordination. SSRN 3924908, 1-77.
[9] Gazda, Vladimir and Horvath, Denis and Resovsky, Marcel (2015). An application of graph theory in the process of mutual debt compensation. Acta Polytechnica Hungarica, 12(3): 7-24.
[10] Fleischman, Tomasz and Dini, Paolo (2021). Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. Journal of Risk and Financial Management, 14(9), 452.
[11] The weight of each edge corresponds to the component \(b_i\) of the net position vector \(\mathbf{b}\) in [10].
[12] To be sure, there can also be firms whose debts exactly balance the credits. Such firms would have a zero net position.
[13] Kiraly, Zoltan and Kovacs, Peter (2012). Efficient implementations of minimum-cost flow algorithms. Acta Univ. Sapientiae, Informatica, 4(1): 67–118.